Konstruktion und Optimierung von Klebeverbindungen für Platten- und Scheibenbauteile aus ultrahochfestem Beton

Geht es um das Zusammenfügen von Betonbauteilen, ist das Kleben noch eine relativ neue Art der Verbindung. Zum kraft- und formschlüssigen Fügen von filigranen Betonfertigteilen eignen sich aber besonders flächige Verbindungen, die durch Verkleben erzielt werden können. Im Teilprojekt des Schwerpunktprogramms SPP 1542 der DFG wurden möglichst einfach zu handhabende Klebeverbindungen für Platten- und Scheibenbauteile konstruiert und optimiert.

Die Verbindungen wurden so ausgelegt, dass sie sowohl Beanspruchungen aus einzelnen Schnittgrößen als auch aus Schnittgrößenkombinationen übertragen können. Dabei wurden folgende Parameter untersucht:

• die Klebefugengeometrie
• die Oberflächenbeschaffenheit
• die Bewehrung der zu verklebenden Bauteile

Optimierungsverfahren

Als Klebstoff wurde in erster Linie ein hochfester mineralischer Mörtel, ein sog. Reactive-Powder-Concrete-Klebstoffe eingesetzt. Das Optimieren der Klebefugengeometrie und der Bewehrung in der Nähe der Fuge erfolgte mit Hilfe eines mathematisch fundierten Shape- und Topologie-Optimierungsverfahrens, wobei die Fugengeometrie sowie das Interface zwischen Beton und Bewehrung mit Level-Set-Funktionen beschrieben wurden.

Dieses Verfahren wurde ursprünglich zur Gewichtsreduktion von Gussteilen entwickelt und nutzt den topologischen Gradienten als Maß für die Sensitivität der Zielfunktion bezüglich der Größe einer Pore oder eines Risses in einem gegebenen Punkt im Bauteil. Auf der Basis der Untersuchungen wurden abgeleitet:

• Entscheidungshilfen zur Fugengestaltung
• ein ingenieurmäßiges Bemessungsmodell zur Berechnung der übertragbaren Schnittgrößen

Herausforderung Zugspannung

Das grundsätzliche Problem beim Verkleben ist die Übertragung von Zugspannungen, da Beton eine relativ kleine Zugfestigkeit besitzt. Während die Zugfestigkeit von Platten durch unterschiedliche Varianten von Bewehrungen erhöht werden kann, werden hier keine Verstärkungen, die die Klebefuge überbrücken, einbezogen.

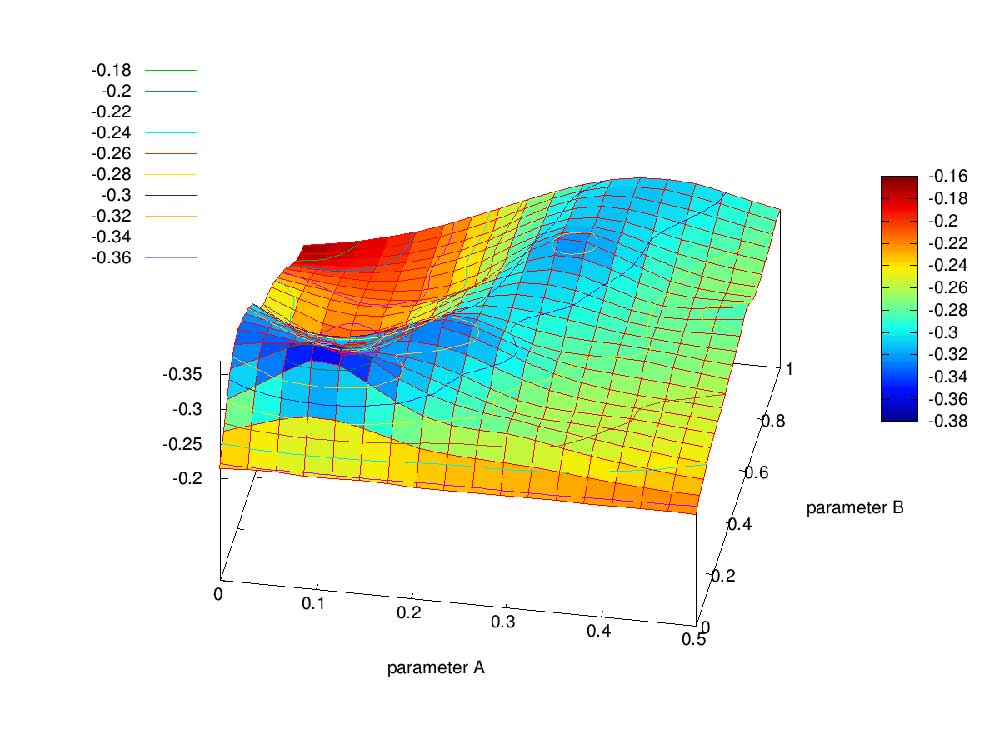
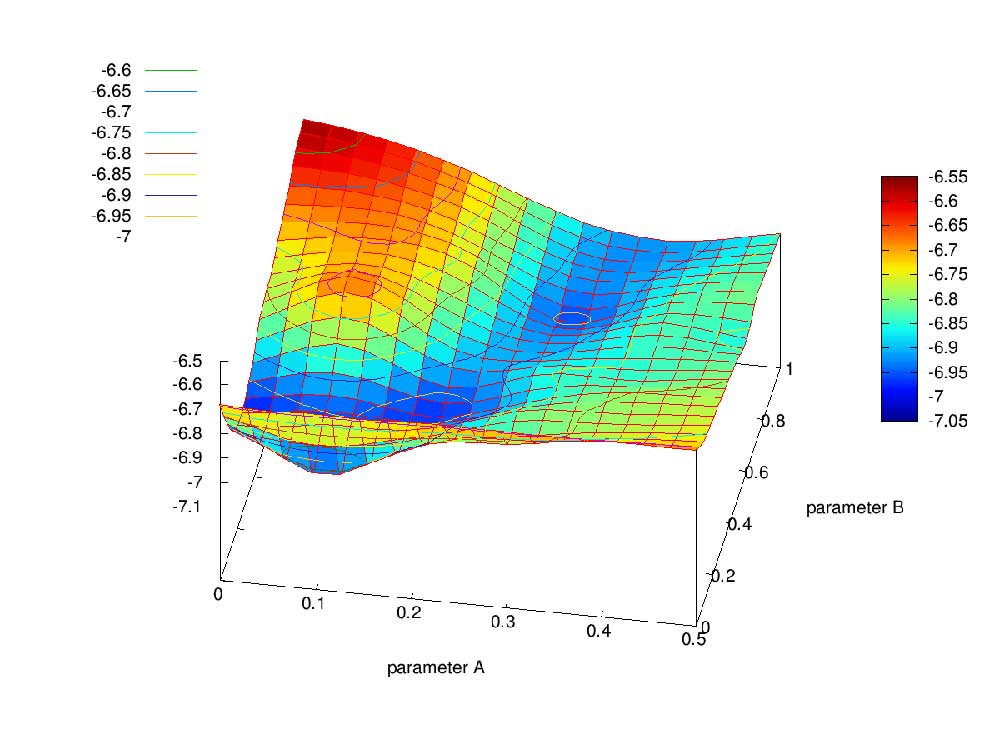
Es werden Fugen mit Zähnen betrachtet, um die aufgebrachten Zugspannungen als Schubspannungen zu übertragen. Zur Bewertung und Optimierung von Klebeverbindungen von HPC-Platten sind genaue Spannungsanalyseverfahren notwendig.

Abgerundete dreieckförmige Zähne optimal

Bei der Shape-Optimierung von Klebefugen ist es sinnvoll, die XFEM zur Strukturanalyse einzusetzen, um die Spannungen und Verzerrungen im Fugenbereich genau zu berechnen und um aufwändige Neuvernetzungen in der Optimierungsschleife zu vermeiden.

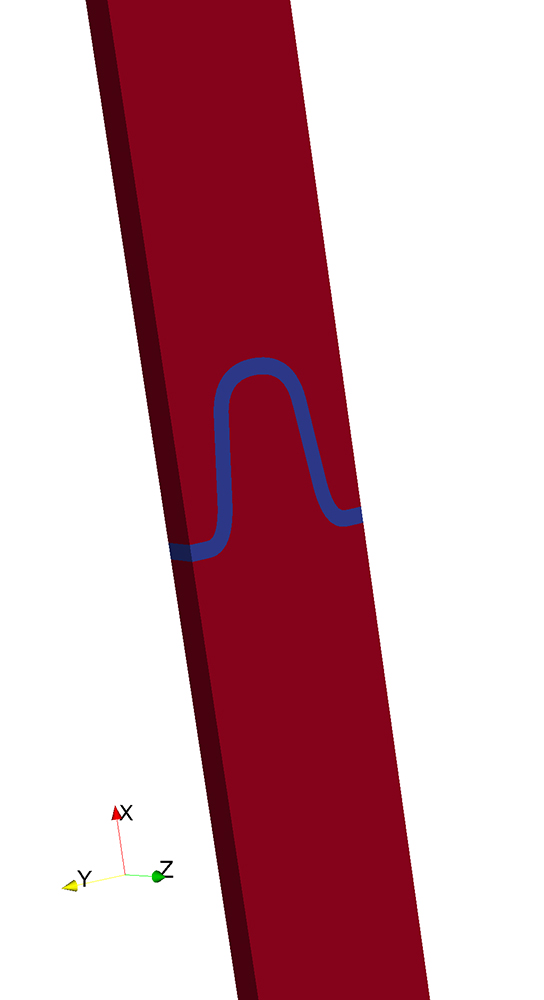
Bei der Topologie- und der Shape-Optimierung wird eine Level-Set-Funktion (siehe Abbildung) zur impliziten Beschreibung der unbekannten freien bzw. zu bestimmenden Materialgrenzen verwendet, so dass eine einheitliche Randbeschreibung bei der kombinierten Topologie- und Shape-Optimierung vorliegt. Das Ergebnis der Shape-Optimierung für die Übertragung von Zugspannungen ist, dass abgerundete dreieckförmige Zähne mit einer großen Tiefe am günstigsten sind.

Die entwickelten Methoden zur Strukturanalyse, Topologie- und Shape-Optimierung sind für beliebige Klebeverbindungen nutzbar. Die beteiligten Materialien können beliebige anisotrope Steifigkeitstensoren besitzen können und beliebige Strukturlasten können betrachtet werden.