Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM
Bei der simulationsgestützten Auslegung von Maschinen oder Anlagen müssen in der Regel auf mehreren Detaillierungsebenen unterschiedliche physikalische Effekte aus Strukturmechanik, Akustik, Wärmetransport, Elektronik etc. erfasst werden (Multiphysics).
Um genaue Vorhersagen zu treffen, wie sich Änderungen von Geometrie oder Materialeigenschaften auf ein einzelnes Bauteil auswirken, bedarf es einer Beschreibung durch partielle Differentialgleichungen, die sich numerisch durch Finite-Elemente-Programme wie ANSYS oder COMSOL behandeln lassen und oft auf große Gleichungssysteme mit vielen Hunderttausend Freiheitsgraden führen.
Um andererseits typische Entwurfsaufgaben wie Geometrieoptimierung, Sensitivitätsanalyse oder Parameteridentifikation für ein System aus mehreren Einzelkomponenten durchführen zu können, ist obiger Zugang bei weitem zu aufwändig. Hier benötigt der Entwickler kleine Zustandsraummodelle mit höchstens einigen Hundert Freiheitsgraden, die das Ein-Ausgabeverhalten der großen FE-Modelle möglichst gut reproduzieren. Auf dieser Abstraktionsebene werden System-Simulatoren wie z.B. MATLAB/SIMULINK eingesetzt.
Ziel: Brücke schlagen
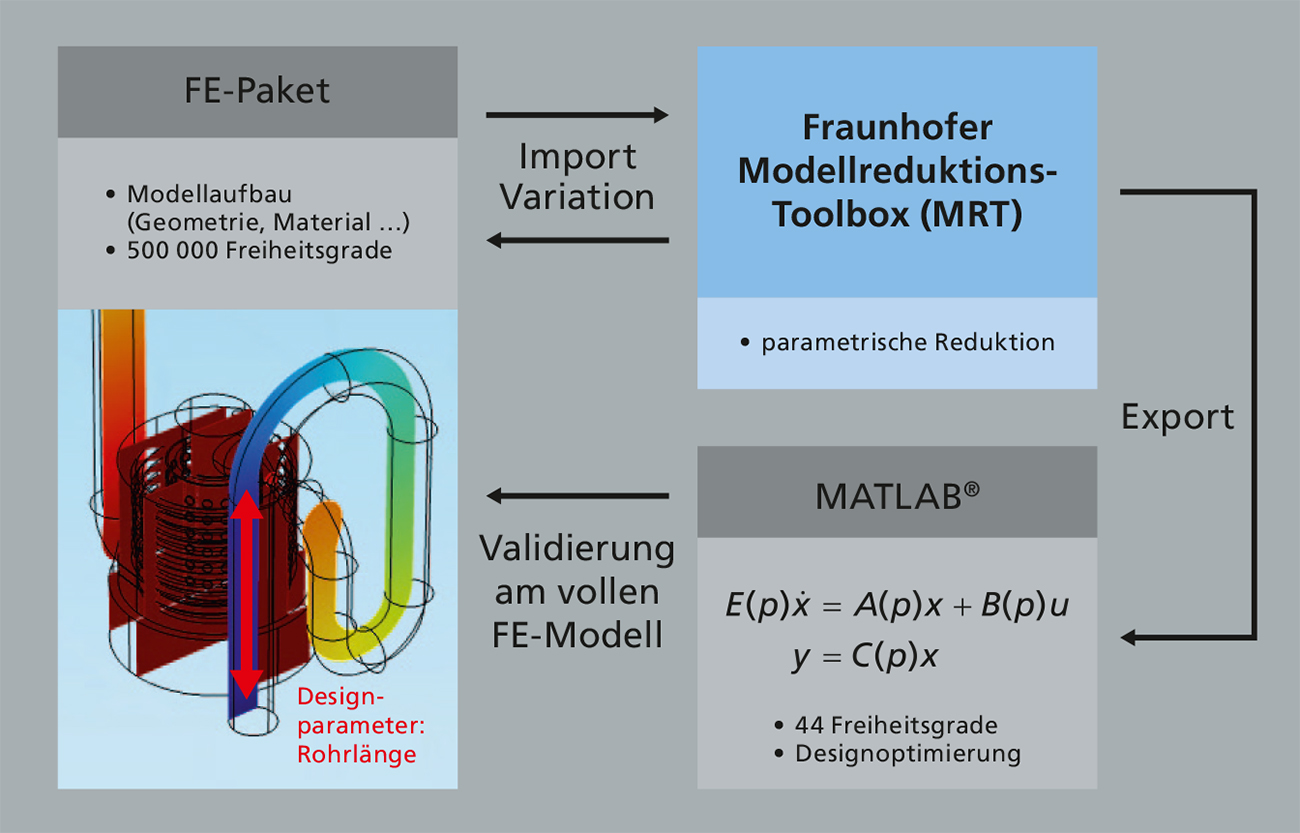
Ziel des Projekts war es nun, eine entsprechende Software (Model Reduction Toolbox) weiterzuentwickeln, die die Brücke zwischen diesen beiden Welten schlägt, d.h. mit der sich einfach und automatisiert FE-Modelle importieren, reduzieren und für die Nutzung in einem Systemsimulator bereitstellen lassen.
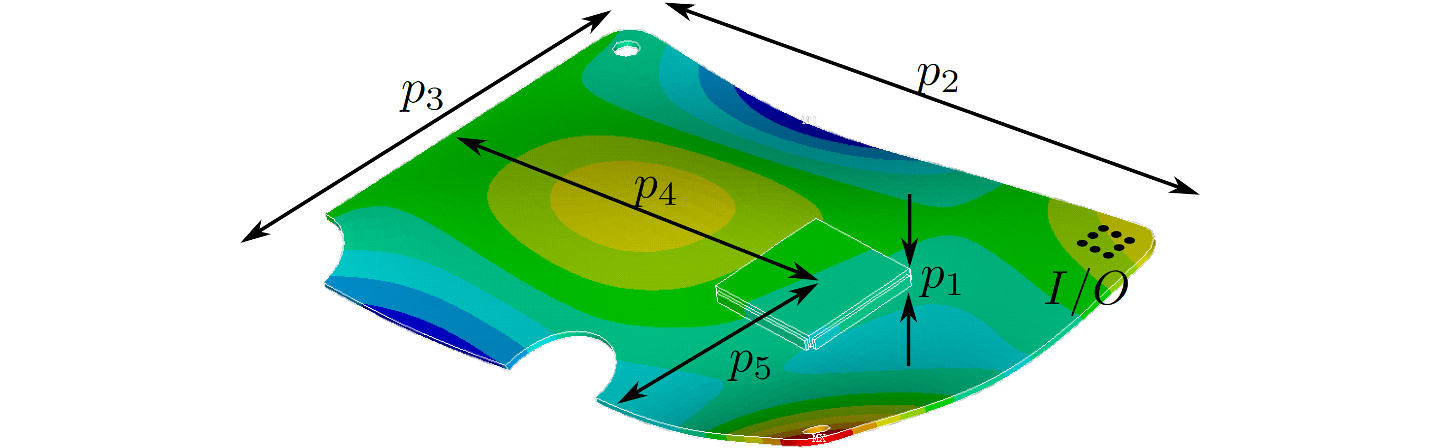
Im Fokus stand dabei die parametrische Modellreduktion: Hängt das ursprüngliche FE-Modell von gewissen Design-Parametern ab, z.B. der Länge eines Rohres, dann bleibt dieser Parameter auch im reduzierten Modell einstellbar. Insbesondere wird vermieden, für jeden neuen Parameterwert erst aus dem geänderten FE-Modell ein neues reduziertes Modell ableiten zu müssen. Im Rahmen einer Parameterstudie oder Optimierung bringt das den entscheidenden Zeitvorteil.
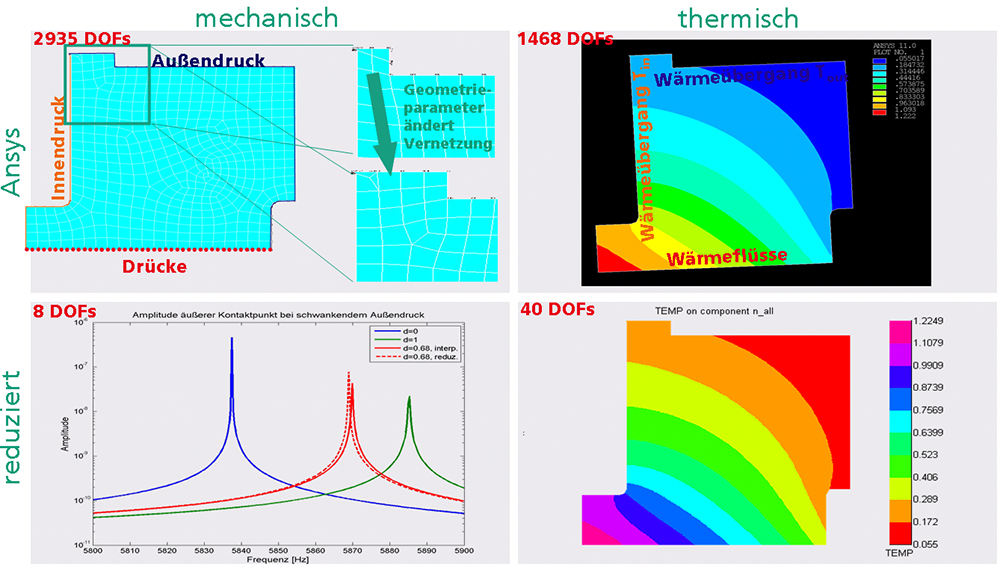
Das verwendete Matrix-Matching-Verfahren hat den Vorteil, dass es auf FE-Modelle anwendbar ist, deren Vernetzungstopologie sich mit den Parametern ändert. Reduzierte Modelle können auch bei unterschiedlich vernetzten Kontaktflächen zusammengesetzt werden.
Projektart: öffentlich gefördertes Projekt
Projektpartner: Stiftung Rheinland-Pfalz für Innovation