© iStockphoto
Unsere Abteilung beschäftigt sich mit der Lösungsfindung zu unterschiedlichsten industriellen Fragestellungen mittels Machine Learning. Sowohl im Bereich des überwachten Lernens als auch im Bereich des unüberwachten Lernens wurde Erfahrung in mehreren Industrieprojekten gesammelt.
Zu unseren Instrumenten zählen u.a.:
Der Einsatz von Methoden zum Deep-Learning bzw. der Verwendung von tiefen Architekturen in Repräsentationsgraphen von Funktionen motiviert sich wie folgt: Theoretische Resultate haben gezeigt, dass Funktionenfamilien (High Level Abstraktionen) z. B. in Objekterkennung, Spracherkennung oder im Text Mining existieren, deren tiefe Repräsentationen exponentiell effizienter sind als flache Repräsentationen.
Wenn eine Funktionenfamilie mit weniger Parametern approximiert werden kann (kleinere VC Dimension), besagt die Lerntheorie (Vapnik 1998), dass man dafür weniger Datenpunkte benötigt. Dies hat Vorteile sowohl in der Berechnungseffizienz (weniger Neuronen), als auch in der statistischen Effizienz (weniger Parameter zu schätzen, mehrfache Nutzung der gleichen Parameter für unterschiedliche Eingänge).
Hastad (1986) hat z.B. gezeigt, dass man O(2d) Parameter und Punkte benötigt, um die so genannte »Parity Funktion« mit d dimensionalem Input mittels traditionellen Machine Learing Algorithmen wie z.B. Gausschen SVM’s oder FF neuronalen Netzen zu approximieren. Um die gleiche Funktion mit einem Deep Neural Network zu approximieren, benötigt man O(d) Parameter und Neuronen in O(log2d) verborgenen Schichten.
Bis 2006 führten Trainingsversuche mit mehrschichtigen neuronalen Netzen zu einer schlechteren Performance (lokale Minima, Sattelpunkte, Overfitting…) in Trainings- und Testdaten als flache Neuronale Netze (mit 1 oder 2 verborgenen Schichten). Dies änderte sich mit den Arbeiten von Hinton (2006) und Bengio (2007), die den Algorithmus »greedy layer wise pre-training« einführten:
Zunächst wird jede Schicht des Modells mittels unüberwachtem Lernen identifiziert und trainiert (Representation Learning RL). Dabei ist jede Repräsentation einer Schicht dann der Input der nächsten Schicht. Abschließend erfolgt mittels überwachtem Lernen ein Fine-Tuning der Parameter aller Schichten mittels Backpropagation zwecks z. B. Klassifikation.
Representation Learning (RL) umfasst eine Sammlung von Methoden, die aus einem Inputvektor automatisch Repräsentationen generiert, die ein anschließendes überwachtes Lernen wie z. B. Klassifikation ermöglichen. »Deep-Learning« Methoden sind RL-Methoden mit multiplen Ebenen, jede Ebene transformiert die vorherige Repräsentation in einen abstrakteren Level angefangen mit den Rohdaten.
Mit anderen Worten: Jede RL-Ebene eines Deep Neural Network versucht ausgehend von der Gültigkeit der Mannigfaltigkeitshypothese (Komplexe Datenmannigfaltigkeiten sind an sich niedrigdimensional) Merkmale zu generieren, die dann z. B. einfacher zu klassifizieren sind. Das heißt, die Variationen entlang der Mannigfaltigkeiten werden detektiert und die orthogonalen Variationen der zur Mannigfaltigkeit tangierenden Räume werden ignoriert. Weiterhin wurde von Bengio (2013) gezeigt, dass die RL-Methode »Auto-encoder« komplexe Datenmannigfaltigkeiten in jedem Layer des Deep Neural Networks entflechtet.
Zurzeit existieren zwei parallel verfolgte Ansätze für RL:
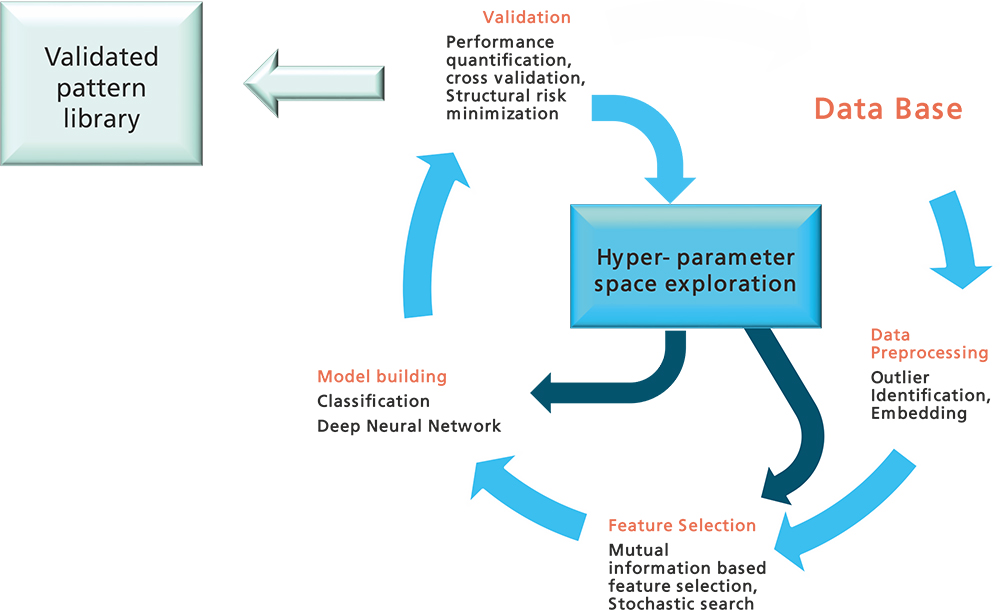
Entsprechende übergeordnete Methoden sind dann »Deep Belief Networks« und »Deep Neuronal Networks«. Der Lernalgorithmus für die RBM, »constructive divergence« (CD) genannt, erlaubt ähnlich wie beim stochastischen Gradientenabstieg ein inkrementelles Update von Batch zu Batch. Hierbei spielt die Wahl der so genannten Hyperparameter eine wesentliche Rolle. Hier nutzen wir »Sequential Model Based Global Optimization« mittels Gaußprozessen und je nach Anwendung mittels Monte Carlo Markov Chain (MCMC).
Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM