The virtualization of chemical manufacturing plants in a model and the subsequent, model-based optimization are key steps towards innovation, as well as for efficiency and quality improvements. The success of this approach crucially depends on the reliability of the models. ITWM and BASF SE are developing, in a bi-lateral cooperation project, hybrid-modeling methods that integrate physical-chemical know-how ("white") with data-driven approaches ("black"). The methods are used at the BASF flowsheet simulator so as to be available for the everyday work of the process engineers.
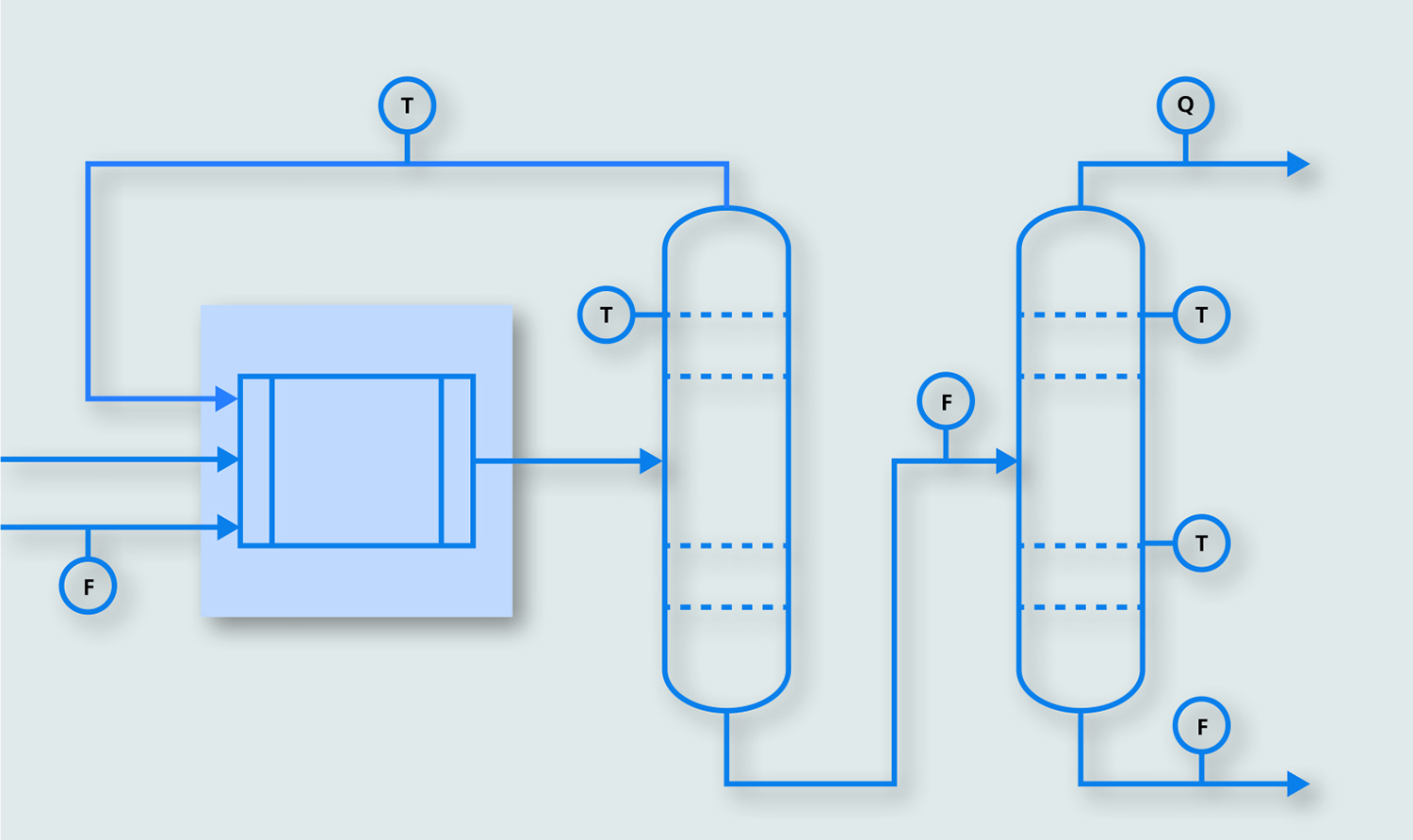
A typical chemical production process includes a chemical reactor for material transformations, with the educt from the reaction being is fed into a purification process, for example, distillation. To model this process in a flowsheet simulator, not only is knowledge of the chemical reactions required, but also the thermodynamics to describe the destillation must be known.
The situation where knowledge of the stoichiometries and reaction constants is incomplete is quite typical in industrial practice, whereas the distillation processes are well known. Besides this physical White Box knowledge, historical process data is available for a variety of measured operating points.
First Step: Short-Cut Model
The goal of the project is to generate information from the process data that can be used to close the gaps of the physical models. To this end, the first step is to replace the reactor with a simplified short-cut model, which contains – together with the purification model – all existing physical equations. The reconciliation performed using the model enable predictions that are as close as possible to the observed measurements for the real plant.