Fraunhofer Institute for Industrial Mathematics ITWM
Fraunhofer Institute for Industrial Mathematics ITWM
Der Erfolg der Medizin hängt von der Vergabeart des Wirkstoffs (Infusion, Spritze, Einnahme) ab.
© iStockphoto
Der Erfolg der Medizin hängt von der Vergabeart des Wirkstoffs (Infusion, Spritze, Einnahme) ab.

Dosage, Effect, Risk

If we want to simulate the distribution of the active substances of a medicine in humans, we have to consider many parameters. Depending on the age or type of administration of the drug, there are deviations, just as each person reacts differently to the drug administered.

© iStockphoto

Mathematics for New Drug Development

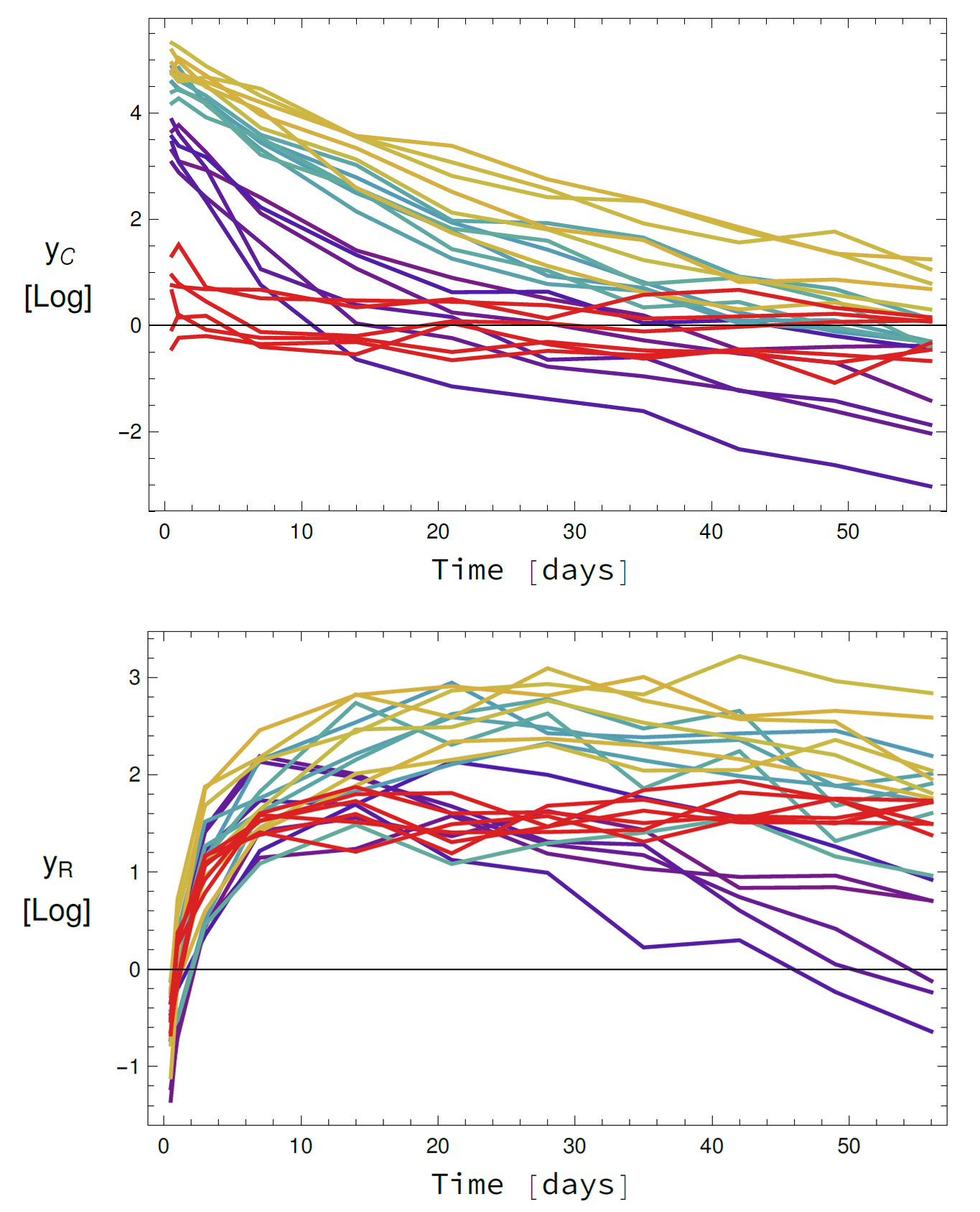
The development of new active ingredients for pharmaceutical purposes is now supported by mathematical learning methods. This capability relates to an important question: What is the proper dosage? The new remedy should work, but not harm the patient. In cooperation with our partner institute, FCC in Gothenburg, we develop and use mathematical simulation and learning methods to find an answer to the question being tested in clinical trials: What is the distribution of active ingredients throughout the body and what effects occur at the targeted sites of action?

In trial testing, as many patients as possible are given different doses of the new drug and the development of the disease in each individual patient is monitored over a long period of time. Monitoring, in this case, means: evaluation of blood samples and body functions. Unfortunately, not all processes in the body can be measured directly.

Zeitliche Entwicklung zweier Stoffkonzentrationen (Wirkstoff und Zielmolekül) im Blutplasma von 24 Patienten, unterteilt in 4 Dosisgruppen zu je 6 Patienten (simulierte Daten).
© Fraunhofer ITWM
Simultierte Daten der zeitlichen Entwicklung zweier Stoffkonzentrationen (Wirkstoff oben und Zielmolekül unten) im Blutplasma von 24 Patienten, unterteilt in 4 Dosisgruppen zu je 6 Patienten (unterschiedliche Farben).

Every Patient is Different

Patients are distinguished by individual characteristics:

  • Gender
  • Age
  • Disease stages
  • Dosages
  • Method of administration of the active ingredient (infusion, injection, ingestion)

Within each of these groups, each person has additional random individual divergences. Here, random means: not everything can happen, just somethings are more probable. This probability can and must be modeled. The administered drug causes a change in the disease-related condition of each patient over time. These time-dependent changes, in turn, affect the probability that other disease-related events will occur. To truly assess how a drug works, such complex relationships need to be understood.

Mathematical Models Master Complexity

Mathematical models are able to capture the complex interrelationships of our bodies, our individual differences, temporal changes, and the changing risk of illness-related events occurring. Initially, however, these models contain many unknown time-dependent and constant variables. We can determine these unknown variables using measured data and the latest computer-aided mathematical learning methods (state filtering and parameter estimation in nonlinear dynamic models with mixed effects). The results provide information about the best dosage and best mode of action of the new drug.

Related Links: