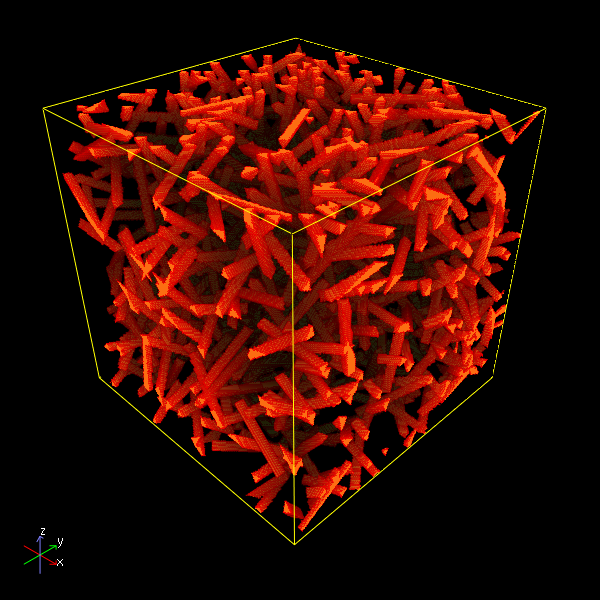
Stochastic geometry models are fit to real structures based on geometric characteristics measured from 3D image data. Varying model parameters creates virtual fiber systems with different microstructures. Consequences on the macroscopic behavior can be studied by numerical simulations
Widely used stochastic models for fibrous structures are Boolean models of cylinders and Poisson processes of dilated lines. For both models, the orientation distribution of the cylinders can be chosen to match the one observed in the materials – isotropic or anisotropic, e. g. with a preferred direction or directions isotropically distributed in a plane.