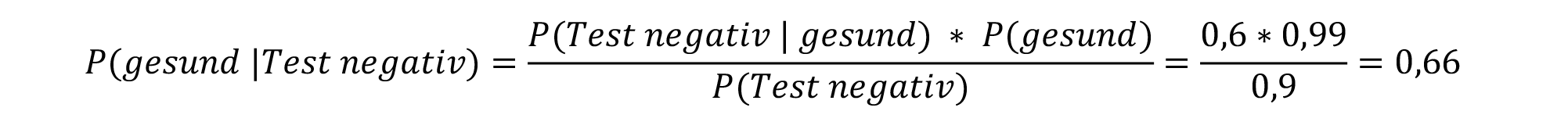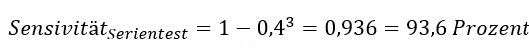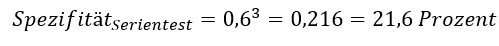Our statisticians Sascha Feth and Jochen Fiedler answer a reader question and blog about statistics and mathematics around the topic of »Reliability of Corona Rapid Tests« in the new Streuspanne post.
© freepik
Last year, we addressed the topic of corona testing and its reliability in a series of blog posts. We received a question from a reader about this series: How much does the reliability of antigen tests increase if you test yourself more than once? Answers are provided by our blogging statisticians Sascha Feth and Jochen Fiedler.
The reputation of antigen testing at testing stations or Corona home self-tests has suffered noticeably recently. This is partly due to findings that rapid tests are less effective in vaccinated individuals because their viral load is only high enough for detection over a shorter period of time. In addition, Omikron has been found to be less readily detected by antigen tests.
In general, however, it has also become known that neither a positive rapid test certainly means infection nor a negative test certainly means the opposite. To be on the safe side, most people therefore repeat a test in case of doubt. Thus, anecdotes about PCR tests that were negative/positive, although one/two/three rapid tests showed positive/negative results, are also accumulating among acquaintances. As an example, we take the following question that reached us as a letter to the editor:
If a [healthy] person tests [negative] three times in a row with a »bad« antigen test whose sensitivity is 60 percent, what is the probability that he »is really healthy«?
In the first sentence, we put »healthier« in parentheses. Here it is not meant as an assumption, because then we would not need to ask about the probability that someone is healthy. Instead, what is meant here is that the person shows no symptoms.
Our choice of words in the first lines of this article was flippant, because THE one reliability does not exist. Instead, we must speak of sensitivity and specificity. If you are not familiar with the two terms, we recommend our mini-series on the subject (see links in the info box).
A sensitivity of 60 percent means that there is a 60 percent probability that a test will be positive in a person with the disease. Now, it's tempting to simply multiply 60 percent by itself three times, which yields 21.6 percent. Supposedly, this number tells you the probability of a sick person getting three positive tests in a row. Spoiler: This statement is not tenable.
Actually, though, the question was about negative test results. If we stick with the sensitivity of 60 percent, a person with the disease is likely to receive a negative test with a probability of 40 percent. Here we would have 6.4 percent as the product.
These figures are not edifying: in just under 78 out of 100 sufferers, not all tests are positive, and in as many as six out of 100 sufferers, not even a single test is positive. So our academic example really deals with a bad test. Presumably, however, one would already react from one positive among the three tests and do a PCR test, for example. The probability for at least one positive among three tests in a diseased person is just the counter probability of »no positive test, given the person is diseased«. There we have 100 - 6.4 = 93.6 percent. Sounds better, but actually our previous calculations are useless anyway.
Useless, because we haven't answered the real question yet (probability that he is really healthy) and useless, because we made untenable assumptions. Because whether the tests are independent is highly questionable.
This is a difficult question and we do not have good data for this either. It would be plausible if the test results are not completely independent. If a test result is positive, the reagents in the test have reacted to something – ideally to viral proteins, in the worse case to some other things. These things may occur randomly in different individuals. For example, it is known that certain foods can promote false-positive results. For false-negative results, one can think of similar effects that are systematic for a single person: For example, the viral load in the throat could be systematically too low in an individual. Either because vaccination has worked very well in that person or because the immune system is generally very good at fighting the pathogen.
Translating these assumptions into mathematical correlations is not possible due to lack of data. What we can do, however, is to investigate the dependence of sensitivity and specificity on the correlations. We'll defer that in detail to a blog post yet to come. In the remainder of this blog post, for simplicity, we will look at the implausible but well-treatable case where the test results are independent.
Back to the original question: You have three independent, negative test results. What is the probability that you are now healthy? To answer this question, it is not enough to know only the sensitivity, i.e. how reliably the test detects diseased persons.
So as the question changes direction, we jump from the concept of sensitivity to that of segregancy. This is another term we introduced in our mini-series. It is the probability that someone who tests negative is actually healthy. However, before we can extend this concept for multiple testing, we must first master the simple test. Without explaining the formula in detail here, we need three probabilities for this:
The first probability is just the specificity of the test. In our reader question, a bad test was given as an example with 60 percent sensitivity. For the sake of simplicity, we adopt this assumption for the specificity. Fortunately, real specificities are much higher. So, with 60 percent probability, I will get a negative test if I do not have the disease. Please note the order:
»{negative test} if {not diseased}« = 60 percent.
To get to the reverse probability, that is, »{not ill} if {negative test}«, we must quantify the other two probabilities.
The second probability – not being diseased – depends heavily on prior knowledge. If we randomly select a person from the population of Germany, then we are probably talking about about 99 percent. However, if this person had contact with infected persons or even had symptoms himself, the probability naturally jumps down uncontrollably. Let us therefore assume that there is no cause or symptoms and set the second probability to 99 percent.
This leaves the probability of a negative test. The data on this are not robust. Not all laboratories report negative tests, especially if they are rapid tests. We can only estimate here that we are above 90 percent. For our sought probability we get thus:
The (made-up) bad test therefore entails that after a negative result we can only assume with a probability of 66 percent that we are healthy.
With a trick we can treat this case analogously to the previous one: We consider the series of three tests one after the other as a separate, larger test, which we will call a serial test in the following. Thus, we now only have to agree on when the series test is positive or negative. The most obvious definition is to define the serial test as negative if all individual tests are negative and positive if this is not the case, i.e. if at least one of the individual tests is positive. The advantage of this definition is that we can now treat this serial test with the known equations, just with a different sensitivity and specificity. The sensitivity results from the counter probability that all three tests of a diseased person are negative.
In formulas:
The specificity of our serial test results analogously from the specificity of the individual tests:
This looks pretty good in terms of sensitivity: Under our independence assumption, sensitivity has increased dramatically, from 60 percent to almost 94 percent! Conversely, however, the specificity has also dropped very sharply – by almost 40 percentage points. For more realistic specificities of about 99 percent, this drop is much less dramatic – there the specificity drops by only 2 percentage points.
Our findings in summary:
With that, let's conclude our considerations of independent test results. In the next blog post, in a few weeks, we will consider in detail the case where test results are dependent.
Fraunhofer Institute for Industrial Mathematics ITWM